擬 potential
An atomic nucleus does not handle an inner core electron of neighboring in an ultimate cause calculation directly, and the 擬 potential (ぎ potential, Pseudopotential) is technique to replace this with the simple potential function for the valence electron. This used that the direct influence of the inner core electron was small in many properties of matter including the bond distance between the atom. When I perform an ultimate cause calculation using a plane wave base, cases to use some kind of 擬 potential for from a problem of the calculation cost are often found.
Such 擬 potential is totally unrelated to the electrostatic interaction and exchange correlative interaction that an inner core electron gives, and it is made for a guideline than a certain radius in the outside by an atomic nucleus only that a wave function agrees with the result of all electron calculations. Therefore, not a thing including the physical approximation and insight such as the mean place approximation, it may be said that it is the temporary technique for calculations to the last. The wave function of the valence band has gnarl (node) in the diameter direction in an atomic nucleus neighborhood, but when I manufacture 擬 potential, I remove such a gnarl and replace a problem secretly so that it is a smooth wave function. Therefore, the wave function (when I use it for the density Pan-function method Kohn-Sham orbit) to be provided by the 擬 potential method may be called 擬波動関数. Such an operation leads to large reduction of the cut-off energy.
Table of contents
Classification of the 擬 potential
擬 potential includes two kinds of the next.
- I am made from experience (this is not an ultimate cause)
- I am made using the result of the ultimate cause calculation
From the precision, the latter is often used now. Because the ultimate cause calculation is high in calculation cost, the manufacture of the 擬 potential is carried out for the atom which is the issue of ball symmetry like the said article exclusively. It is a problem complicated in itself in this way how available the 擬 potential that manufactured it is to an atom of solids including chemical bond. In the property of the problem, the clear answer does not exist; almost with the calculation cost balance. The 擬 potential not to cause a problem even if I fit various solids is expressed saying "trans ferrabooby tea is high".
Problems of the 擬 potential
Problems on using 擬 potential are that the technique using the 擬 potential becomes powerless virtually in properties of matter (inner husk excitation, core level shift) that an inner husk electron participates in to ignore the contribution of the inner husk electron (the trial that is going to handle a core level shift by 擬 potential technique exists). In addition, in the ような situation that the contribution of the inner husk electron influences properties of matter under very high pressure (value computerization of the inner husk electron), the band calculation by the 擬 potential cannot cope either. Because 擬波動関数 does not express the wave function in the inner core domain about the calculation of the optics reply appropriately either, a problem occurs.
But I assume where an inner husk electron, and arbitrariness remains whether you handle from where as a valence electron. For example, I can use technique of the 擬 potential as a valence electron by a slight inner husk electron including the 3d orbit of gallium. By such handling, I can take the effect from the inner husk orbit in a calculation partially, too.
擬 potential of the fermi
Enrico Fermi introduced 擬 potential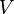
to describe the dispersion of the free neutron by the atomic nucleus. [1] I suppose that the wave function of the remote neutron is expressed with the scattered wave of the s wave expressed by a spherical wave and the sum with the incidence plane wave distantly by a dispersion body. Thus, the potential is given by the function 
of the radius vector.
As for the 
Planck's constant をで
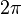thing which I broke,
as for the mass,
as for the delta function of the D rack,
the neutron dispersion head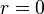
is a nuclear center of gravity here. [2] The shape factor of the neutron is provided by the Fourier transform of this 
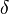function.
About the dispersion of the neutron by the atomic nucleus having one above. I can write the fermi 擬 potential when a dispersion body is many systems as follows.
The 擬 potential that is made from experience
擬 potential by the ultimate cause
Allied item
Quotation
- ^ E. Fermi (July 1936), "Motion of neutrons in hydrogenous substances," it is Ricerca Scientifica 7: 13–52
- ^ Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications (1996) ISBN 0-486-69447-X
This article is taken from the Japanese Wikipedia 擬 potential
This article is distributed by cc-by-sa or GFDL license in accordance with the provisions of Wikipedia.
In addition, Tranpedia is simply not responsible for any show is only by translating the writings of foreign licenses that are compatible with CC-BY-SA license information.
0 개의 댓글:
댓글 쓰기