Resolving power
The resolving power (ぶんかいのう, Optical resolution) is the measurement or the ability that I can distinguish in an object in devices. I include a microscope, a telescope, resolving power and the resolution in the diffraction grating.
Table of contents
Definition in the optical microscope
The resolving power by the optical microscope is defined with two points of resolving power. The resolving power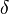
of two point light sources according to the standard of レーリー,
となる. Maximum angle, n for the optical axis of the rays that open number of persons, θ of the object lens are incident on an object lens from an object as for λ in wavelength, NA of the light here are refractive indexes of an object and the medium between the object lens. It is said that I can resolve around 0.2 micrometers if I use an object lens of magnification 100 times of 油浸 with a visible ray. However, this is not a limit because the limiting value of resolving it changes by illumination condition and imaging system. The diffraction limited of the lens may be used in the meaning that is equal to resolving power, but is not right for a definition of the resolving power.
Definition in the scanning type probe microscope
With the scanning type probe microscope, the definition is not decided.
It is said that I have atom resolving power because an irregularity equivalent to every the lattice of the atom of the single-crystal sample is got under the good measurement condition in the scanning tunnel microscope.
Attention is need for interpretation of the expression of the resolving power in the microscopic catalogue and article that there is only the method that does not know contrast mechanism in the assay that there is multiple of the scanning type power microscope including the atomic force microscope, and it looks like it. Resolution near a scanning tunnel microscope is realized with the non-contact atomic force microscope to perform in ultrahigh vacuums and can resolve an irregularity equivalent to every the lattice of the atom of the insulator.
Definition in the electron microscope
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png){kind=small} | The correction of this knob is expected. |
Definition in the telescope
Two points are defined at an angle of a minimum to distinguish. The resolving power
of two point light sources including 2 double stars is, for example, standard によればである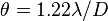
of レーリー. 
The wavelength of the は light is diameter of 
object lens. The theory resolving power of the astronomical telescope of 100mm is 1.3 "degree, and the diameter of object lens is equivalent to distance of approximately 2.4km on the surface of the moon that I looked at from the ground. By the astronomical telescope, an expression of Dors (W.R.Dawes) is used and demands it at resolving power = 116"/-caliber. In addition, the general formula from low magnification is found in resolving power = 40" ×√( diameter / magnification +1) / diameter + (82/ diameter). If it is magnification 20 times as diameter 100mm, it becomes 1.16" at 5.72", magnification 150 times.
Definition in the spectroscope
In the spectroscope, I express the ability that can isolate the spectral line of two of them approaching it and,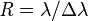 
and, am defined. 
Is the difference of 2 wavelengths to be able to understand for は; the mean wavelength.
Definition in the diffraction grating
The resolving power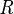
of the diffraction grating is equal to the lattice line number of diffraction gratings 
and the order of diffraction
product.
Definition in the prism
The resolving power of the prism is given in the length of the base of prism side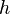 
and the product 
of the dispersion.
Definition in the interference spectroscope
Allied item
This article is taken from the Japanese Wikipedia Resolving power
This article is distributed by cc-by-sa or GFDL license in accordance with the provisions of Wikipedia.
In addition, Tranpedia is simply not responsible for any show is only by translating the writings of foreign licenses that are compatible with CC-BY-SA license information.
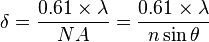
0 개의 댓글:
댓글 쓰기