Hyper graph

The example of the hyper graph: ,.

I performed generalization (expansion) of a graph in the mathematics, and an edge (branch) can connect a node (top) of any number with the hyper graph (British: Hypergraph). It is expressed a dove by a pair to say formally, and a meeting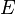 of the elements called a node or the top is a meeting of the subsets that is not a hyper edge (hyperedge) and an empty set of being called it. Therefore,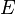 it is はの subset and is はの power set. The edge of the normal graph is expressed by the pair of two nodes, but the hyper edge is expressed with the set of any node and includes the node of the option unit.

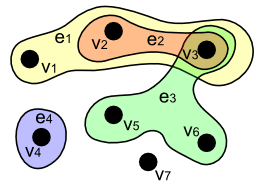
Unlike a graph, it is difficult for the hyper graph to illustrate it in a newspaper. Therefore an illustration such as the graph theory is rarely done and tends to be expressed by a term of set theory.

Summary

Many theorems of the graph theory hold good by the hyper graph. Typically, there is a theorem of Ramsey. I am expanded, and the study on symmetricalness of the graph can apply to a hyper graph, too. When a hyper graph is the associate same model, there is the representation from the top set of a certain hyper graph to it which is different, and one edge means the thing corresponding to other edge. When a hyper graph is the same model, I say the case that is the associate same model to the reverse. When a hyper graph is the self-same model, the top meeting that a top meeting added a label to again means that it is the associate same model. Self-set H (= (X, E)) of the hyper graph of the same type Oh, it becomes the group about composition and call it with self-same model group of the hyper graph and is expressed in Aut(H). I shoot the group of the hyper graph and am the area consisting of meetings of the としての hyper graph associate same model.

"Crossing" (transversal) of hyper graph H = (X, E) or "a hitting set" (hitting set) is the meeting that a product meeting is empty with no edge. In other words, a common node exists between T and each edge by all means. It is said that crossing T is "a minimum" when there is not a thing to be able to call crossing as the truth subset. "A crossing hyper graph" of H is a hyper graph expressed in (X, F), and F consists of all smallest crossing of H. The calculation of the crossing hyper graph is applied in the field of comp-sci such as the machine learning and the theory of games, the index of the database are dated it and are related to the issue of sufficiency possibility, optimization.

I call the hyper graph that the density of each edge (the original number) is k "k equality" (k-uniform) or "k hyper graph" (k-hypergraph). A graph is the hyper graph that 2 is the same. Degree d(v) of top v is the number of the edge which the top belongs to. It is said that the degree of all tops is "k Masanori" by the hyper graph which is k (k-regular).

It is said that there is here. There are all hyper graph にはの "incidence matrices" (incidence matrix), and the following is managed.

It should be hyper graph をの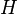 "双対" defined by the dislocation line of the incidence matrix (dual), and, oh, a set consisting of the causes of the m unit is a set consisting of subsets of one of n unit. とについてであるときのみである. 双対 of the same hyper graph is Masanori, and the reverse is satisfied, too. There is often new discovery by thinking about 双対.

Coloring of the hyper graph

The coloring of the hyper graph is defined as follows. という hyper graph はであるとする. I point to be the coloring that がの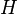 is proper when it becomes on any top about one of all.

Allied item

• Bare meeting
• The division of the meeting
• Limited crossing-over characteristics
• Top coating

This article includes the text of item hypergraph of creative Commons license indication - succession 3.0 non-transplant online mathematics dictionary "PlanetMath" contributed to

It is acquired by "https://ja.wikipedia.org/w/index.php?title= hyper graph &oldid=57469524"

This article is taken from the Japanese Wikipedia Hyper graph

This article is distributed by cc-by-sa or GFDL license in accordance with the provisions of Wikipedia.

Wikipedia and Tranpedia does not guarantee the accuracy of this document. See our disclaimer for more information.

In addition, Tranpedia is simply not responsible for any show is only by translating the writings of foreign licenses that are compatible with CC-BY-SA license information.